Home

Solving Difficult Problems

Abductive reasoning is similar to reasoning by analogy - the process of equating a well-understood thing with a poorly-understood thing in order to solve a difficult problem that could not be solved directly. In effect, analogy substitutes important characteristics of the known thing for those of the unknown, based on the similarity of their shared characteristics.

In fact, examples of analogy abound in economics and physics, such as using an analogy of a circulatory system as a stand in for economy or using the abstraction of a perfect gas to model stellar dynamics or the Big Bang. Most modeling and simulation techniques are to some extent practical applications of reasoning by analogy, and they often work very well in predicting the behavior of things that can not be measured directly.

Case Based Reasoning

Another important and very practical application of abduction is "Case Based Reasoning". CBR has a rough and ready concept of degree of matching or 'distance' between examples of some thing. The 'Case' in CBR take a legal turn when searching a large database of rulings and precedents whose characteristics match those of a current legal case. CBR has practical application in product design and engineering as well.

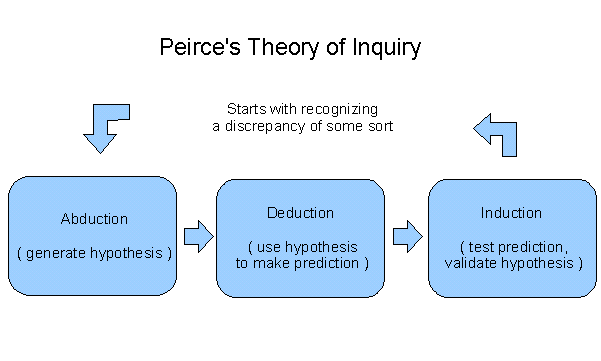
Peirce's Theory of Inquiry: Multi-Modal Inference

A great American philosopher of the late 19th century, Charles Peirce, discovered a neat system to explain how the three mode of inference work together to drive the process of scientific inquiry. The Wikipedia has a good description of Peirce's Theory of Inquiry.

In the roughest terms, abduction is what we use to generate a likely hypothesis or an initial diagnosis in response to a phenomenon of interest or a problem of concern, while deduction is used to clarify, to derive, and to explicate the relevant consequences of the selected hypothesis, and induction is used to test the sum of the predictions against the sum of the data.

These three processes typically operate in a cyclic fashion, systematically operating to reduce the uncertainties and the difficulties that initiated the inquiry in question ... the purpose of abduction is to generate guesses of a kind that deduction can explicate and that induction can evaluate.

The basic flow of the inquiry and discover process is illustrated in the diagram.

{ Example of above}

So ... Is Socrates a Cat or Not ?

Using the previous example where we concluded that "Socrates is a cat", one could further deduce that since "Socrates is a cat" and "All cats have four legs" ( most cats anyway ), Socrates must also have four legs. This is a hypothesis that can be confirmed or rejected based on inductive inference. If we observe that Socrates only has two legs, then the hypothesis deduced from "Socrates is a cat" can be rejected.

Observation:

Rule:

Conclusion:
Socrates has two legs

All cats have four legs

Therefore it is NOT true that Socrates is a cat

( The hypothesis is rejected )

Note that the logical expression is in the form "NOT Socrates is a cat", rather than saying "Socrates is not a cat". This is one of the irreducible complexities of logic which will become critical in the design of an engine to automate or 'externalize' the process of inference. For now, note that from a logical perspective, saying "NOT Socrates is a cat" is distinct from saying "Socrates is not a cat", that is, "Socrates is a cat" is false and "Socrates is not a cat" is true.

The steps outlined above are a rough approximation of a rigorous environment, but it looks as if a pragmatically formulated set of inference tools can be made simple and intuitive enough for everyday people to use solving complex reasoning problems.