Abduction: Inference with an Attitude
The final form of inference is abduction often called ( somewhat falsely ) by the name of " false deduction". However, abductive inference it is not always false.
Abduction is the "guilt by association" mode of inference. The question of deduction is not "what logical conclusions can I infer" but rather "does it have a certain something ?". The abductive form of the classical expression:
| Observation: | Socrates is mortal |
| Rule: | All men are mortal |
| Conclusion: | Therefore Socrates is a man |
A diagram of this inference would look like:
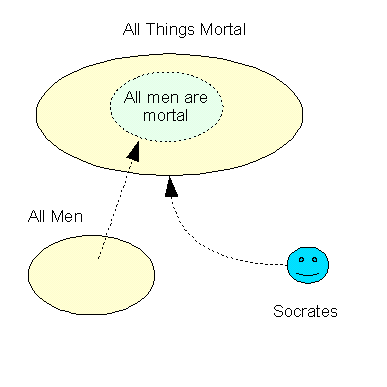
It is tempting to say that the exclude middle is the quality of being mortal, except it is not really the middle but the ends of the assertions that are being excluded. Returning to the ABC form of inference, the 'excluded ends' principle of inference could be expressed as:
IF A -> C,
ALL B -> C
THEN A -> B USUALLY FALSE !
The reading would be that "if two things share a quality, it means that the are same thing", which may be true occasionally, but is far more likely to be false most of the time. In the case above, the association between Socrates and men happens to be correct, since after all is said, Socrates is a man.
But why not substitute another true assertion about "All somethings" and see how it works.
| Observation: | Socrates is mortal |
| Rule: | All cats are mortal |
| Conclusion: | Therefore Socrates is a cat |
Graphically it could be represneted as:
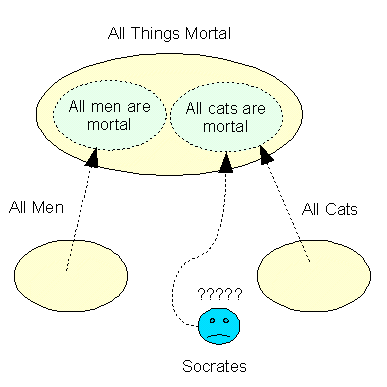
The 'excluded ends' are the quality of being mortal, arriving at the erroneous conclusion that "Socrates is a cat". If the rule were stated as 'only cats are mortal', then the inference that "Socrates is a cat" would be inescapable, if still untrue.
