Home

Most of classical Greek logic is based on the principle of the excluded middle. The basic structure is an observation, a rule and a conclusion. The most famous example of a logical expression is the deduction:

A graphic representation of the rule with a Venn diagram.

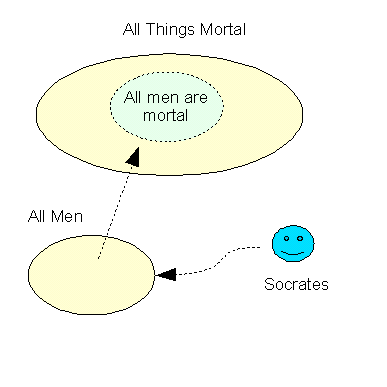
The excluded middle in the case of deduction is the term "men", inferring that Socrates must necessarily share in the mortality of all men. Another way to express the idea is:

Socrates -> Man,
All Men -> Mortal,
Therefore assert that Socrates -> Mortal

In a more universal form, the principle of the excluded middle can be expressed as:

IF A -> B,
ALL B -> C
THEN A -> C

This holds true for anything true statement that can be inserted into slots A, B and C. Assuming that the two premises are true and that one sticks to the meaning of ALL B -> C, then by the laws of deductive logic, the conclusion is guaranteed to be true, every time.

There are some extra details about what can actually be inferred when the relationships ( -> ) between A, B and C are of certain types, such as inheritance of characteristics or ownership of something else. Another complication is when "some" rather than "all" of B has a relationship to C and one can legitimately infer that NOT ALL B -> C. Obviously, it can become very complex, even with a small number of assertions. It's a involved subject, to be covered with more details in later sections.

Logical Chaining

Exact deductive inference of this kind forms the backbone of most inference engines in rule based systems. If the observations are actually 'true' and and the rules are stated in an exact manner, then the inference engine work exactly as intended. Of course, there are the pragmatic problems of ensuring the truthfulness of the observations and the precision of the rules. However, in principle, deductive rule engines should work as advertised.

Deduction the Only Valid Form of Reasoning

Of the three forms of inference in rule based systems, deductive logic is the only universally 'valid' form of logic. Deductive logic moves from the specific to general, inferring 'true' assertions about the nature of things in the world from 'true' ences of these assertions.

The other two forms are inductive and abductive inference: they are capable of producing inexact and even unexpected conclusions. Induction moves backward from the specific to the general, inferring from consequences to implied causes. Abduction moves kind of laterally, that is from general to specific as in the case of deductive inference, but by the process of association of characteristics rather than by identifying membership in some category. This is why abduction is often called false deduction.

It is the other two forms of inference that can give 'exact' logic a bad name.