| 2.2 Logical Inference |
| Home | Business Rules | Rule Based Systems | Rule Engines | Semantic Web | Links | Under the Hood |
| The Ubiquity of Logical Inference
The Fuzziness of Everyday Language
|
Feb 3 2009: A more recent version of the article can be found at the business rules site. All people utilize some form of logical inference in their everyday lives - buying things, crossing the street, solving a problems at work, preparing dinner. Yet how many people have actually examined the the way they go about using logical inference ? Very few. The term 'logical inference' may conjure up an image of crusty academics furiously splitting hairs over the obvious, perhaps with some justification. But sometimes what seems obvious is not all that obvious. It's a result of the difference between logic and language. Logic is precise and everyday language is imprecise. People like the fuzziness of language - it can bestow deep significance upon common things ( like toothpaste or soap ) or allow us to give answers which sound meaningful but are utterly devoid of meaning, as the situation requires. There is a warm and fuzzy feeling about everyday language because it works for us in ways that logic does not. Language is riddled with fuzzy logic that helps to describe the fuzziness of human situations and experiences. However, communicating with machines requires a logical type of language, one with sufficient precision to accomplish useful tasks in a predictable way. To speak the language of rules, one must master the rigors of basic logic. This requirement is frequently underplayed by companies selling business rule tools and methodologies. They tend to paint a picture of a brave new world where business people rather than programmers encode business logic for transaction processing systems. While the business rules approach shifts the focus from arcane computer languages to a more natural way of expressing business logic, that does not free business people from having to understand how logic works, quite the contrary. The next few sections are a sort of 'logical boot camp', perhaps reviving memories of a sleepy afternoon in a high school or college math course many years ago. After reviewing the basics of logic, the following sections discuss the three mode of logical inference. |
|
||||
|
The Basics
Venn Diagrams
Visualizing rules
|
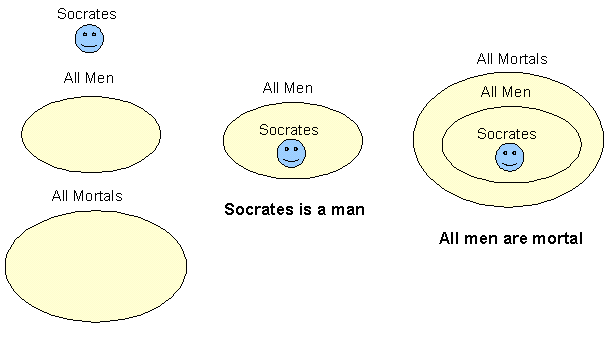
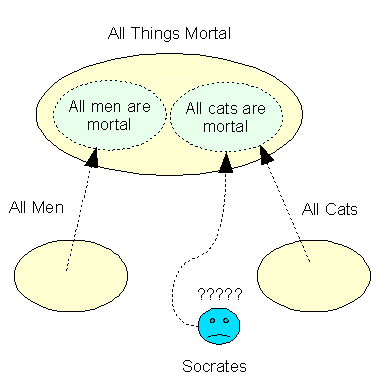
Much of the complexity of a collection of rules arises from interactions between logical expressions within the rules ( also called logical 'terms' ). Unless rule base designers work assiduously to simplify rule expressions, they will be rapidly overwhelmed by the complexity of the rule base. One of the most powerful tools available to rule base designers to help simplify complex rule expressions is Venn Diagrams. The idea is simple - every example of something in the world can be put inside of a circle. It helps rule base designers to visualize the consequences of rules. For instance, there is the most classically Greek or all logical expressions is: Socrates is a man The same expression in Venn Diagram form is:
The deduction appears to be almost trivial when the terms are expressed in a diagram. It's like big fish swallowing little fish ( that just swallowed Socrates ) The deduction can also be expressed in a more general form ( the "ABC" form ). IF A is a B This expression is valid for anything that can be placed into slots A, B and C.
|
|||||
|
Logical Expressions
AND, OR, XOR
|
Frequently, expressions are in a different form than a simple
construction of terms "A AND B", where both must be true for
the expression to be true. There may be cases where either "A
OR B" can be true for an expression to be true.
For example, a store might have a policy about their days of business with a rule that days of operation are "weekdays and Saturdays", in other words they are closed on Sundays. Note that using everyday language, the rule would be expressed as "weekdays AND Saturdays", which means that the store will never open because there will never be day which is both a weekday and a Saturday. A precise expression in a more constrained rule format would be something like "IF day = aWeekday OR day=aSaturday THEN StoreOpen = true". In everyday language, the word "AND" usually means add the two together, as in the case of "weekdays and Saturdays". The logical definition of the word AND is saying "when the two are true together", which means that when either one is false, the two are rejected. In other words, a logical AND works more like subtraction than addition. The logical OR effectively add the two groups together. The diagram below show the adding and subtracting behavior of logical OR and AND, with the help a new category "Things Named Socrates", including people, pets, computer applications, anything denoted by the word 'Socrates'.
The diagram for the OR expression shows all things in the world named Socrates ( people, pets, whatever ) plus all men in the world, and all women too ( ancient Greek philosophers must have intended to include women in their propositions as well ). This diagram demonstrates an almost visual sense of addition, as if a logical OR were merging visual layers in a drawing. The AND expression shows the only those things in the world which are both men and named Socrates ( not pets ). In the caseo fthe AND construction, there is a sense of subtracting out anything that is not common between the two visual layers. The third diagram shows an example of a common logical expression, the XOR ( eXclusive OR ) expression. It is saying "things which are either named Socrates or are men, but not both named Socrates and are men. In fact, it is the exact equivalent of saying "A OR B AND NOT ( A AND B ). In the sense of a visual analogy, iIf you take the OR expression on the left and subtract the AND expression in the middle, you can derive the XOR on the right.
|
|
||||
| Using NOT in Expressions |
The use of NOT in logical expressions can complicate set of a rules very
quickly. To express the behavior of the NOT operation In Venn
Diagram form requires creating of new element, that is a rectangle
representing a universe of all possible things.
Note that evaluating the expression in the middle yields 'all things named Socrates that are not men", including pets and computer applications, but not people. The expression of the right shows a new feature of logical expression that goes under various names - bracketing, closure, etc. It says "evaluate the expression between the parenthesis first and then evaluate the outside expression". As you can see, adding the parenthesis to the expression "All Men AND Things Named Socrates" alters the meaning considerably. In fact, the use of parenthesis to control evaluation order is discouraged in rule base design. The alternatives will be discussed in the section "Rule Base Design".
|
|||||
|
Overview of the Three Modes of Inference
Deduction
Induction
Abduction
Deduction the Only Valid Form of Reasoning
Developing a Working Set of Tools
A Hammer and Tongs Approach to Logical Inference
|
The three modes of logical inference are deduction, induction and
abduction. At this point it may be may be helpful to look at
formal definitions of the terms. The Wikipedia defines deductive reasoning as:
The Wikipedia defines inductive reasoning as:
The Wikipedia defines abductive reasoning as:
Of the three forms of inference in rule based systems, deductive logic is the only universally 'valid' form of logic. Deductive logic moves from the specific to general, inferring 'true' assertions about the nature of things in the world from 'true' ences of these assertions. The other two forms are inductive and abductive inference: they are capable of producing inexact and even unexpected conclusions. Induction moves backward from the specific to the general, inferring from consequences to implied causes. Abduction moves kind of laterally, that is from general to specific as in the case of deductive inference, but by the process of association of characteristics rather than by identifying membership in some category. In fact, abduction is often called false deduction. The assertions of these two modes of forms of inference may or may not be 'true' according to the circumstances - certainly, they can never be 'true' with the absolute metaphysical certainty characteristic of logical deduction. The meaning of 'inferring from consequences' is discussed in the following sections. Note that the definitions presented below are overly broad and might even be considered eccentric from the exacting perspective of classical and modern mathematical logic. The intention is not to probe the deep inner workings of mathematical logic but to develop a set of workable set of tools to solve common problems. The definitions given below might legitimately be said to represent a 'hammer and tongs' approach to using logical inference in rule based systems ( when it works at all ).
|
|||||
|
Deduction
|
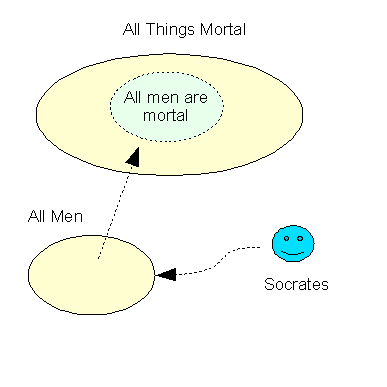
Most of classical Greek logic is based on the principle of the excluded
middle. The basic structure is an observation, a rule and a
conclusion. The most famous example of a logical expression is the
deduction:
The excluded middle in the case of deduction is the term "men", inferring that Socrates must necessarily share in the mortality of all men. Another way to express the idea is: Socrates -> Man, In a more universal form, the principle of the excluded middle can be
expressed as: This holds true for anything true statement that can be inserted into slots A, B and C. Assuming that the two premises are true and that one sticks to the meaning of ALL B -> C, then by the laws of deductive logic, the conclusion is guaranteed to be true, every time. There are some extra details about what can actually be inferred when the relationships ( -> ) between A, B and C are of certain types, such as inheritance of characteristics or ownership of something else. Another complication is when "some" rather than "all" of B has a relationship to C and one can legitimately infer that NOT ALL B -> C. Obviously, it can become very complex, even with a small number of assertions. It's a involved subject, to be covered with more details in later sections. Exact deductive inference of this kind forms the backbone of most inference engines in rule based systems. If the observations are actually 'true' and and the rules are stated in an exact manner, then the inference engine work exactly as intended. Of course, there are the pragmatic problems of ensuring the truthfulness of the observations and the precision of the rules. However, in principle, deductive rule engines should work as advertised. It is the other two forms of inference that can give 'exact' logic a bad name.
|
|||||
|
Induction
|
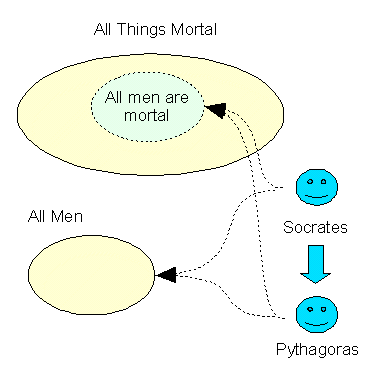
Expressed in the inductive form, the same set of assertions about
Socrates would be:
The exclude middle is Socrates, linking Men and quality of being mortal. But clearly there is a problem here. There is an implicit assumption that Socrates represents all men or more explicitly, "Man is Socrates". We know that is not true but, nonetheless, this sort of inference seems to occur quite often in everyday language as over-generalizations. In fact, we could equally associate "men and "mortals" in the other direction and conclude that "All mortals are men", based on the sole example of Socrates. What does this mean ? One way to interpret it is by reading the conclusion as "Based on what we know about Socrates, there is no reason to reject the assertions that "all men are mortal" or that "all mortals are men". Disproving the notion that "all mortals are men" is an easy task - the first mortal bird or squirrel encountered along the highway would disprove it beyond doubt. However, the only way to prove finally and forever the mortality of all men is to examine every human on earth ( including Pythagoras ) and determine the presence or absence of mortality in their set of personal characteristics. Clearly. it is an impossible task since there would always be the possibility of someone being born who just might disprove the ancient assertion. In this sense, induction can never prove anything beyond all doubt, only very high degrees of likelihood. The mathematical laws of probability can set an upper limit on the likelihood of error, ( assuming that the experimental method was correct, which is not always the case ). In the case of the assertion that "all men are mortal", it is as certain as any truth we know. Even as rough 'guesstimate', one can say that the chance of error is no more than one in many billions ( the 'true' probability of error is much smaller, of course ). Induction by experimentation is the basis of the scientific method and knowledge discovery. Most rigorous statistical and numerical-intensive techniques fall into the inductive mode. There are many effective models and methods for inductive learning, such neural networks and various types of associative networks. The results of these models may be difficult to interpret, but they are easy to use these days. An important feature of inductive inference is capability to measure precisely the degree of error in associating data from a large population with the generalized rule. This is in stark contrast to the abductive mode of inference.
|
|||||
|
Abduction
False Deduction
|
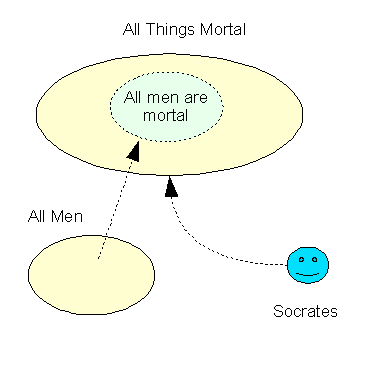
The final form of inference is abduction. Abduction is the
"guilt by association" mode of inference. The
abductive form of the classical expression:
It is tempting to say that the exclude middle is the quality of being
mortal, except it is not really the middle but the ends of the
assertions that are being excluded. Returning to the ABC form of
inference, the 'excluded ends' principle of inference could be expressed
as: The reading would be that "if two things share a quality, it means that the are same thing", which may be true occasionally, but is far more likely to be false most of the time. In the case above, the association between Socrates and men happens to be correct, since after all is said, Socrates is a man. But why not substitute another true assertion about "All somethings" and see how it works.
The 'excluded ends' are the quality of being mortal, arriving at the erroneous conclusion that "Socrates is a cat". If the rule were stated as 'only cats are mortal', then the inference that "Socrates is a cat" would be inescapable, if still untrue.
|
|||||
|
Real World Abduction
Classification
Abduction as an Early Warning System
Reasoning by Analogy
Case Based Reasoning
|
Of course, identifying things by a single characteristic is not the way
abductive inference works in the real world. Someone performing a
classification task would use a full set of 'relevant' characteristics
in order to identify Socrates as either a man or a cat. Does he
have fur, how many legs does he walk on, etc. There would be a
rough sense of fitness of the match between the characteristics of the
thing and the categories being tested, sometimes expressed as a
"distance function" between the thing being tested and the
ideal. There might also be a scoring mechanism to put greater
weight on certain matches. For instance, a match to 'feathers'
would probably have a higher scoring weight than 'skin' - Socrates could
only be a a bird.
Abduction is the Great Classifier of reasoning. The phrase "if it looks like a duck and it quacks like a duck then ..." is a classically abductive statement. As attractive as it sounds, this is not a valid mode of reasoning - it is the result of association of characteristics between two subjects, maybe with some practical screening mechanism to improve the chances of success. It is neither a true deduction nor a valid statistical induction about the relationships between the subjects themselves. If false deductions are invalid, why do we keep doing it ? We do it because it works well of us, as it has for many millions of years. The old adage, "where there's smoke there must be fire" is a perfect example of a cautionary abductive inference and may provide a hint as to why the abductive mode of inference holds such power over our cognitive processes. It's an early warning system and often a very effective one. Abductive reasoning is similar to reasoning by analogy - the process of equating a well-understood thing with a poorly-understood thing in order to solve a difficult problem that could not be solved directly. In effect, analogy substitutes important characteristics of the known thing for those of the unknown, based on the similarity of their shared characteristics. In fact, examples of analogy abound in economics and physics, such as using an analogy of a circulatory system as a stand in for economy or using the abstraction of a perfect gas to model stellar dynamics or the Big Bang. Most modeling and simulation techniques are to some extent practical applications of reasoning by analogy, and they often work very well in predicting the behavior of things that can not be measured directly. Another important and very practical application of abduction is "Case Based Reasoning". CBR has a rough and ready concept of degree of matching or 'distance' between examples of some thing. The 'Case' in CBR take a legal turn when searching a large database of rulings and precedents whose characteristics match those of a current legal case. CBR has practical application in product design and engineering as well.
|
|||||
|
How the Three Modes of Inference Work Together
Peirce's Theory of Inquiry
|
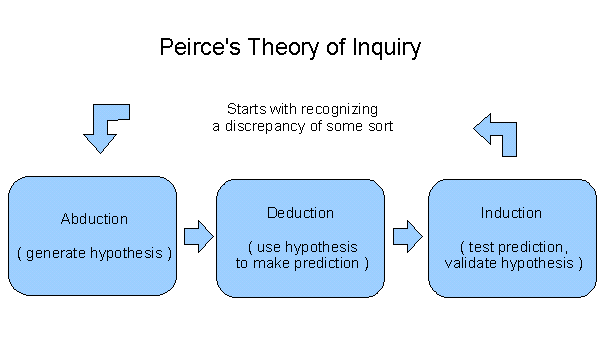
A great American philosopher of the late 19th century, Charles Peirce,
discovered a neat system to explain how the three mode of inference work
together to drive the process of scientific inquiry. The
Wikipedia has a good description of Peirce's Theory of Inquiry. In the roughest terms, abduction is what we use to generate a likely hypothesis or an initial diagnosis in response to a phenomenon of interest or a problem of concern, while deduction is used to clarify, to derive, and to explicate the relevant consequences of the selected hypothesis, and induction is used to test the sum of the predictions against the sum of the data. The basic flow of the inquiry and discover process is illustrated in the diagram.
Using the previous example where we concluded that "Socrates is a cat", one could further deduce that since "Socrates is a cat" and "All cats have four legs" ( most cats anyway ), Socrates must also have four legs. This is a hypothesis that can be confirmed or rejected based on inductive inference. If we observe that Socrates only has two legs, then the hypothesis deduced from "Socrates is a cat" can be rejected.
Note that the logical expression is in the form "NOT Socrates is a cat", rather than saying "Socrates is not a cat". This is one of the irreducible complexities of logic which will become critical in the design of an engine to automate or 'externalize' the process of inference. For now, note that from a logical perspective, saying "NOT Socrates is a cat" is distinct from saying "Socrates is not a cat", that is, "Socrates is a cat" is false and "Socrates is not a cat" is true. The steps outlined above are a rough approximation of a rigorous environment, but it looks as if a pragmatically formulated set of inference tools can be made simple and intuitive enough for everyday people to use solving complex reasoning problems.
|
|||||
|
|
||||||
|
<<< |
|